اي الاعداد التاليه عدد غير نسبي

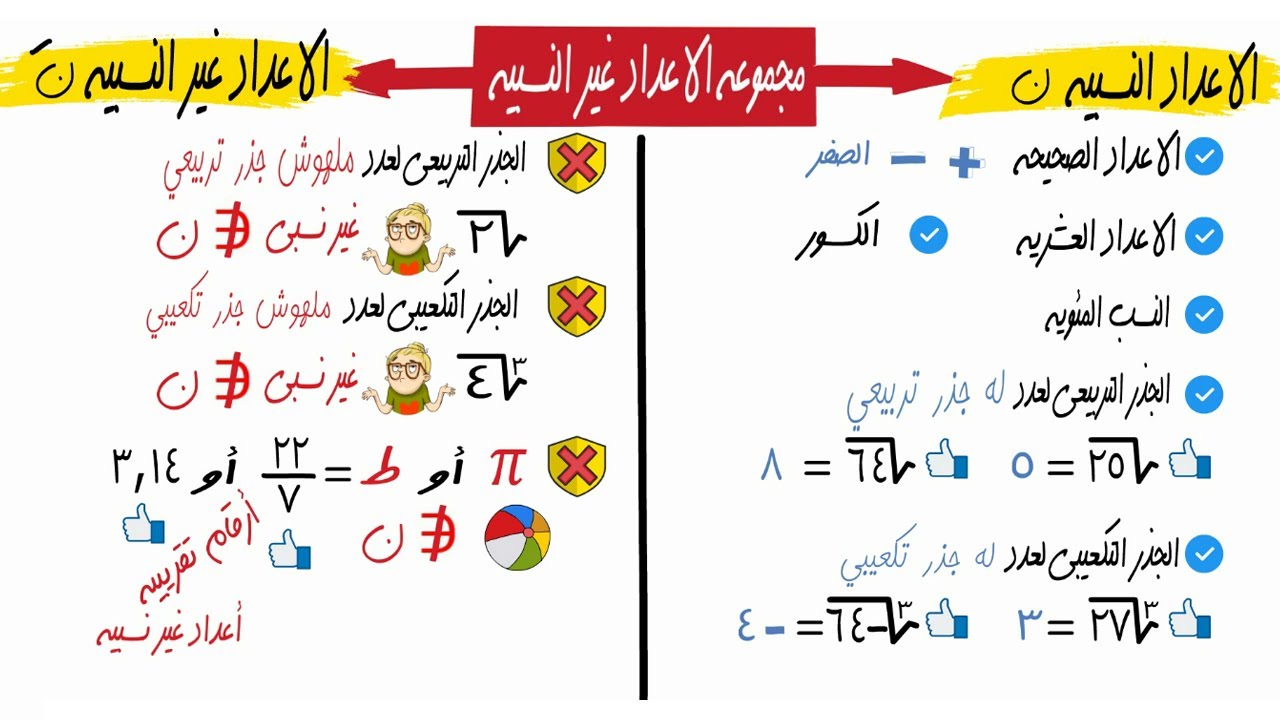
الأعداد غير النسبية

مقدمة

الأعداد غير النسبية هي أعداد عشرية غير نهائية وغير دورية، بمعنى أنها لا يمكن كتابتها كنسبة عددين صحيحين. وتشمل الأعداد غير النسبية جميع الأعداد الجذرية مثل الجذر التربيعي لـ 2 والجذر التكعيبي لـ 3، وكذلك الأعداد المتسامية مثل π و e.

خصائص الأعداد غير النسبية

الأعداد غير النسبية غير قابلة للتمثيل كنسبة عددين صحيحين.

الأعداد غير النسبية لها تمثيل عشري غير منته وغير دوري.

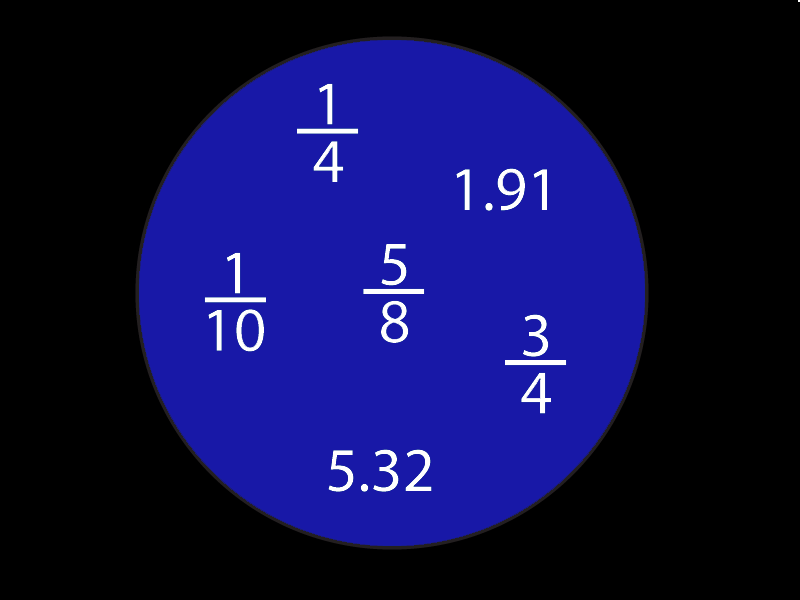
الأعداد غير النسبية لا يمكن تقريبها بدقة تامة.

أمثلة على الأعداد غير النسبية

الجذر التربيعي لـ 2 (√2)

الجذر التكعيبي لـ 3 (³√3)

العدد π (نسبة محيط الدائرة إلى قطرها)

العدد e (أساس اللوغاريتم الطبيعي)

عدد ذهبي (1.618…)

استخدامات الأعداد غير النسبية

تُستخدم الأعداد غير النسبية في العديد من مجالات الرياضيات، بما في ذلك الجبر والهندسة والتحليل.

تُستخدم الأعداد غير النسبية في تطبيقات العالم الحقيقي، مثل الحوسبة والفيزياء والمالية.

أنواع الأعداد غير النسبية

الأعداد الجذرية: هي الأعداد التي يمكن كتابتها كجذر عدد صحيح، مثل √2 و ³√3.

الأعداد المتسامية: هي أعداد غير جذرية لا يمكن كتابتها كنسبة عددين جبريين. ومن الأمثلة على الأعداد المتسامية π و e.

التمثيل العشري للأعداد غير النسبية

التمثيل العشري للأعداد غير النسبية غير منته وغير دوري.
يمكن تقريب الأعداد غير النسبية إلى أي درجة من الدقة باستخدام تمثيلها العشري التقريبي.

خصائص العمليات الحسابية على الأعداد غير النسبية

جمع الأعداد غير النسبية ينتج عنه عدد غير نسبي.

طرح الأعداد غير النسبية ينتج عنه عدد غير نسبي.

ضرب الأعداد غير النسبية ينتج عنه عدد غير نسبي.

قسمة عدد نسبي على عدد غير نسبي ينتج عنه عدد غير نسبي.

الخلاصة

الأعداد غير النسبية هي مجموعة من الأعداد العشرية غير المنتهية وغير الدورية. وهي تشمل الأعداد الجذرية والأعداد المتسامية. للأعداد غير النسبية خصائص وتطبيقات فريدة في مجالات الرياضيات المختلفة والتطبيقات في العالم الحقيقي.