حل المعادلات ذات الخطوة الواحدة ثالث متوسط

المعادلة ذات الخطوة الواحدة هي معادلة جبرية تحتوي على متغير واحد ومصطلح واحد فقط على كل جانب من علامة التساوي. لإيجاد حل المعادلة، فإننا نقوم بالعكس العمليات الجبرية التي أجريت عليها.
خطوات حل المعادلات ذات الخطوة الواحدة
1. جمع أو طرح نفس العدد من كلا الجانبين

إذا أضفنا أو طرحنا نفس العدد من كلا الجانبين، فإن قيمة المتغير لا تتغير.


2. ضرب أو قسمة كلا الجانبين بنفس العدد غير الصفري

إذا ضربنا أو قسمنا كلا الجانبين بنفس العدد غير الصفري، فإن قيمة المتغير لا تتغير أيضًا. ومع ذلك، يجب توخي الحذر عند قسمة كلا الجانبين بصفر لأن ذلك سيؤدي إلى حل غير محدد.
3. عزل المتغير على جانب واحد من علامة التساوي
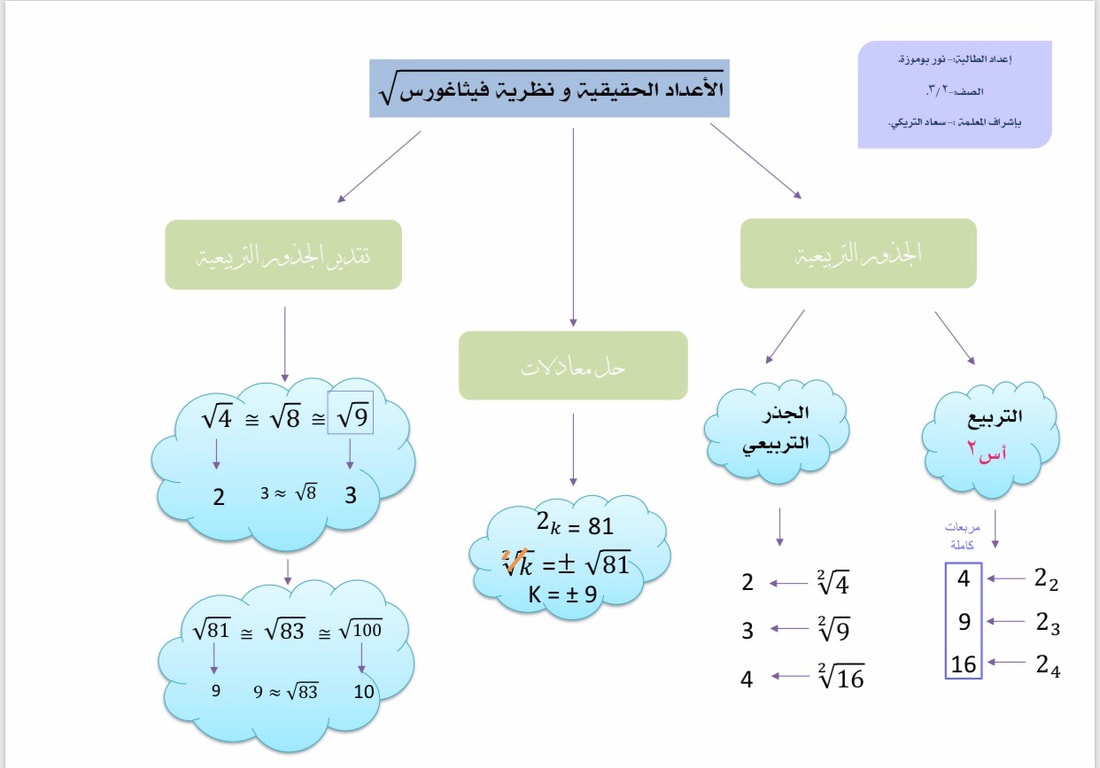
الهدف النهائي هو عزل المتغير على جانب واحد من علامة التساوي. يمكننا القيام بذلك عن طريق تطبيق الخطوات السابقة.

طرق حل المعادلات ذات الخطوة الواحدة

1. الجبر

يتضمن الجبر استخدام العمليات الجبرية لحل المعادلات. نبدأ بمعادلة بسيطة ثم نطبق خطوات حل المعادلات عليها.

2. الرسم البياني
يمكننا رسم المعادلة بيانيًا بإيجاد نقاط التقاطع مع المحور س والمحور ص. قيمة المتغير هي الإحداثي السيني لنقطة التقاطع مع المحور س.
3. التحليل بالجداول
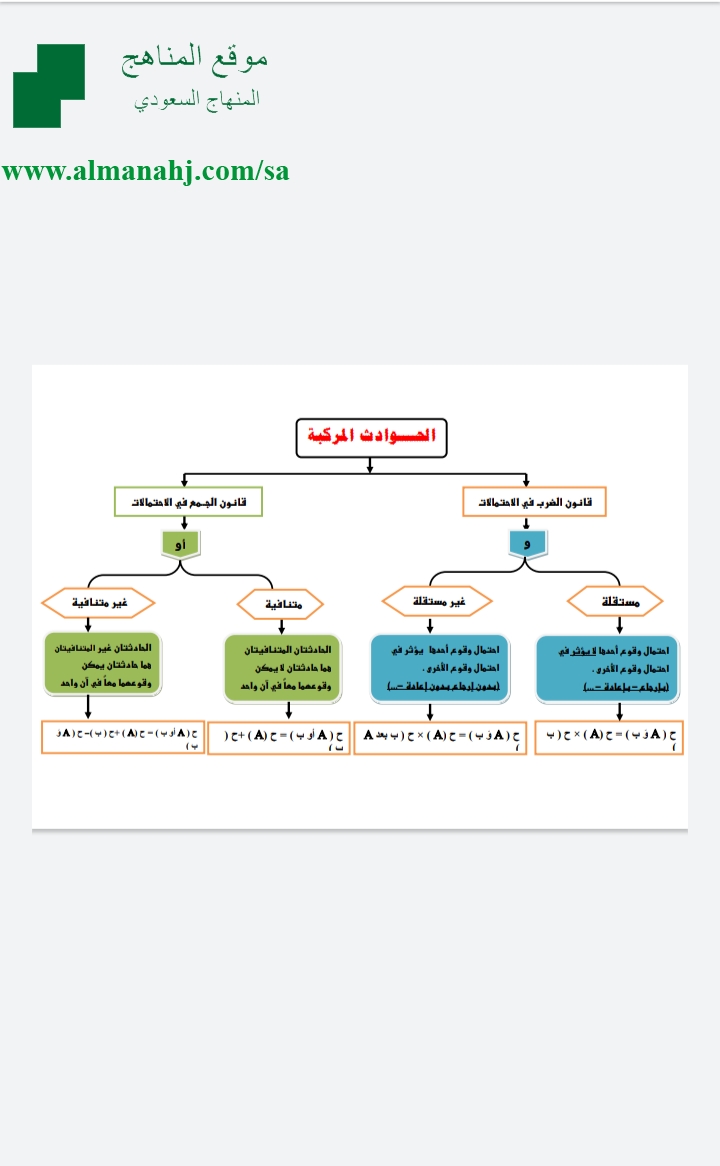
ننشئ جدولًا لقيم مختلفة للمتغير ونستبدلها في المعادلة. تساعدنا القيم التي تجعل المعادلة صحيحة في تحديد حل المعادلة.
تطبيقات المعادلات ذات الخطوة الواحدة
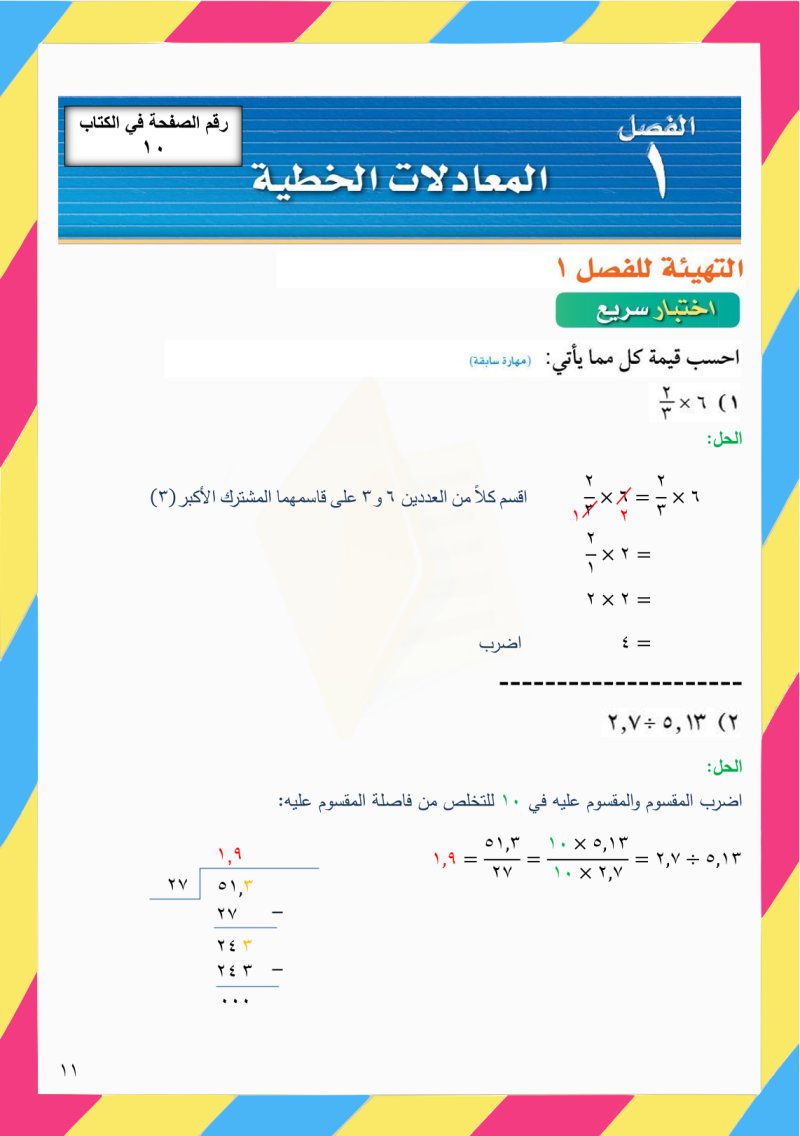
1. حل المسائل الواقعية
يمكننا استخدام المعادلات ذات الخطوة الواحدة لحل المسائل الواقعية التي تتضمن متغيرات غير معروفة.

2. التمثيل البياني
تستخدم المعادلات ذات الخطوة الواحدة لتمثيل العلاقات الخطية بيانيًا. يساعدنا الرسم البياني على فهم العلاقة بين المتغيرات.
3. النمذجة الرياضية

تستخدم المعادلات ذات الخطوة الواحدة في النمذجة الرياضية لوصف الظواهر المختلفة. تساعدنا النماذج على التنبؤ بسلوك الأنظمة والعمليات.

أمثلة على حل المعادلات ذات الخطوة الواحدة
1. جبر
حل المعادلة: 2x + 5 = 11

2x = 6

x = 3
2. رسم بياني

حل المعادلة: y = 2x + 1

الرسم البياني هو خط مستقيم مع ميل 2 واعتراض ص 1. نقطة التقاطع مع المحور س هي (0.5).

3. تحليل بالجداول

حل المعادلة: x – 3 = 5

x المعادلة

——
0 -3 = 5 خاطئ

1 -2 = 5 خاطئ
2 -1 = 5 خاطئ

3 0 = 5 خاطئ
4 1 = 5 خاطئ
5 2 = 5 خاطئ
6 3 = 5 خاطئ

7 4 = 5 خاطئ

8 5 = 5 صحيح
إذن، الحل هو x = 8.
خاتمة
حل المعادلات ذات الخطوة الواحدة هو مهارة أساسية في الجبر. من خلال اتباع الخطوات وطرق الحل المناسبة، يمكننا حل المعادلات ذات الخطوة الواحدة بثقة واستخدامها في مجموعة متنوعة من التطبيقات.