علامة اكبر من واصغر من

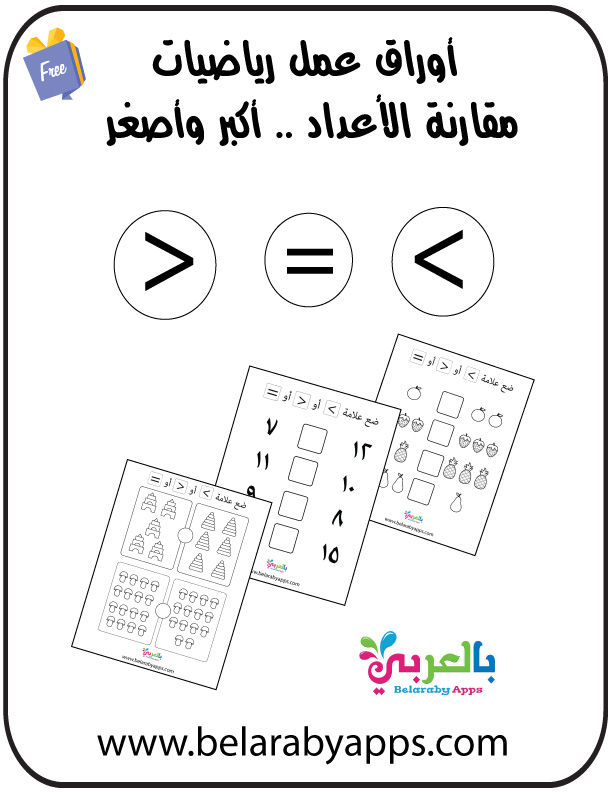
علامة أكبر من واصغر من

رمزا أكبر من و أصغر من هما رمزين رياضيين شائعان يستخدمان للمقارنة بين قيمتين. تُكتب “أكبر من” على شكل (>)، وتُكتب “أصغر من” على شكل (<).

رموز وعلامات المقارنة الرياضية

بالإضافة إلى “أكبر من” و”أصغر من”، تتضمن رموز المقارنة الأخرى ما يلي:

يساوي (=)


أكبر من أو يساوي (≥)

أصغر من أو يساوي (≤)

لا يساوي (≠)

استخدام “أكبر من” و”أصغر من”

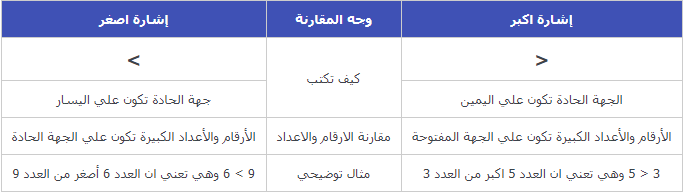
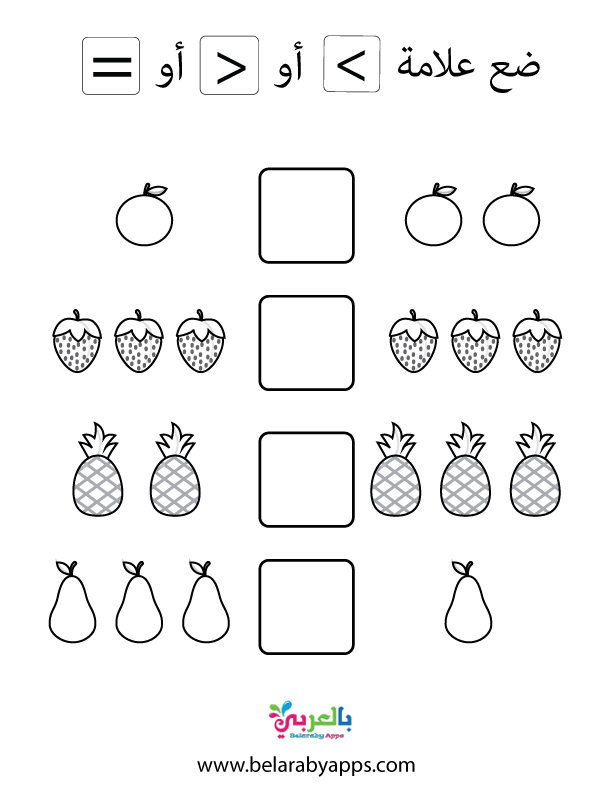
تُستخدم علامتا المقارنة “أكبر من” و”أصغر من” لإجراء مقارنة بين قيمتين. إذا كانت القيمة الموجودة على يسار الرمز أكبر من القيمة الموجودة على اليمين، فإن المقارنة صحيحة. وإذا كانت القيمة الموجودة على يسار الرمز أصغر من القيمة الموجودة على اليمين، فإن المقارنة غير صحيحة.

أمثلة

5 > 3 (5 أكبر من 3، لذا فإن المقارنة صحيحة)

2 < 7 (2 أصغر من 7، لذا فإن المقارنة صحيحة)
4 ≥ 4 (4 أكبر من أو يساوي 4، لذا فإن المقارنة صحيحة)
1 ≤ 3 (1 أصغر من أو يساوي 3، لذا فإن المقارنة صحيحة)

6 ≠ 8 (6 لا يساوي 8، لذا فإن المقارنة صحيحة)

قواعد المقارنة

هناك بعض القواعد الهامة التي يجب مراعاتها عند إجراء المقارنات:

يمكن فقط مقارنة القيم من نفس النوع (على سبيل المثال، الأعداد مع الأعداد، والمتغيرات مع المتغيرات).

لا يمكن مقارنة القيم المتباينة (على سبيل المثال، الأعداد مع المتغيرات).

يتم إجراء المقارنات من اليسار إلى اليمين.

تطبيقات علامتي “أكبر من” و”أصغر من”

تُستخدم علامتا “أكبر من” و”أصغر من” في العديد من المجالات، بما في ذلك:

الرياضيات

العلوم

الحوسبة

الحياة اليومية

أمثلة

في الرياضيات، تُستخدم علامات المقارنة لحل المتباينات.

في العلوم، تُستخدم علامات المقارنة لتحديد ما إذا كان أحد المتغيرات أكبر أو أصغر من متغير آخر.
في الحوسبة، تُستخدم علامات المقارنة لإجراء عمليات المقارنة المنطقية.

في الحياة اليومية، تُستخدم علامات المقارنة لمقارنة الأشياء مثل الأسعار والأحجام والأوزان.

المتباينات

المتباينة هي معادلة جبرية تتضمن علامة مقارنة. يمكن أن تكون المتباينات بسيطة أو معقدة، ويمكن استخدامها لتمثيل مجموعة متنوعة من العلاقات بين المتغيرات.

أمثلة

x > 5 (x أكبر من 5)
y ≤ 10 (y أصغر من أو يساوي 10)

2x – 1 < 3 (2x ناقص 1 أصغر من 3)

القيم القصوى والدنيا

القيمة القصوى هي أكبر قيمة ممكنة لمتغير في مجموعة معينة. القيمة الدنيا هي أصغر قيمة ممكنة لمتغير في مجموعة معينة.

أمثلة

القيمة القصوى لـ x إذا x < 10 هي 9.

القيمة الدنيا لـ y إذا y ≥ 5 هي 5.
القيمة القصوى لـ z إذا 2z + 1 ≤ 11 هي 5.

الخاتمة

علامتا “أكبر من” و”أصغر من” هما رموز رياضية مفيدة تُستخدم لإجراء المقارنات بين القيم. يتم استخدام هذه العلامات في مجموعة واسعة من المجالات، بما في ذلك الرياضيات والعلوم والحوسبة والحياة اليومية. من خلال فهم قواعد المقارنة وتطبيقات علامتي “أكبر من” و”أصغر من”، يمكنك استخدامها بفعالية لحل المشكلات واتخاذ القرارات.